[논문리뷰] LORA: LOW-RANK ADAPTATION OF LARGE LANGUAGE MODELS

 

Large Language Model (LLM) 을 사용하기 위해서는 고성능의 GPU 가 필요합니다. 그러나 현재 가장 성능이 좋다고 알려진 NVIDIA의 A100 한 개의 가격은 거의 싯가로 적용이 되며 2,500 만원에서 3,000 만원 사이로 거래되고 있습니다.

그런데 만약 저희 같은 일반인이 이것을 사용하려고 하기엔 너무나 큰 금액이기에 프로젝트를 진행할 수 가 없습니다. 그래서 찾아 보게된 기술이 GPU를 조금 효율적으로 쓸 수 없을 까? 라는 궁금증에서 찾아보게 된 LoRA를 소개 시켜드리려고 합니다. LoRA 는 Low-Rank Adaptation 의 줄임말이며, 구글에 LoRA: Low-Rank Adaptation of Large Language Models 를 검색하면 논문을 찾을 수 있습니다.

 

 

Introduction

자연어처리는 많은 응용은 pre-trained LLM을 down stream 응용으로 적응 시키는 것에 의존합니다. 비유를 하자면 대규모 공장인데 범용적인 생산 설비를 가지고 있어서 여러 종류의 제품을 만들 수 있는 것 입니다. 여기서 하위 작업(down stream)에 적응 시킨다는 말은 여러 종류의 제품을 만들기 위해서 공장 시설을 정비하고, 필요한 부품을 조립하는 과정이라고 할 수 있습니다.

 

다시 LLM으로 돌아와서 이런한 적응들은 일반적으로 pre-trained 모델의 모든 매개변수(parameters)를 업데이트를 하는 방식으로 미세조정 (fine-tuning) 을 합니다. 이러한 fine-tuning 모든 매개변수를 업데이틀 하게 되면 한번 프로그램을 돌릴 때마다 컴퓨팅 파워 낭비가 심해지므로 효율이 떨어진다고 볼 수 있습니다. 거기에 더해서 요즘 나오는 LLM 모델 같은 경우에는 훨씬 많은 parameter를 가지고 있기에 이런 부분은 단점이라고 할 수 있습니다.

 

이렇나 단점을 보완하기 위해 일부 매개변수만 조정하거나, 새로운 작업에 대해 외부 모듈을 학습한는 방식으로 시도를 했서 효율성을 증가 시켰습니다. 그러나 모델의 깊이를 확장시켜 추론 지연 (inference latency) 가 생기거나, 사용할 수 있는 시퀀스의 길이가 짧아지는 단점이 있습니다.

앞선 선행 연구에서 LLM의 많은 매개변수 안에서 실제로 모델이 학습하는 중요한 정보는 low intrinsic dimension 에 존재한다는 것을 밝혔습니다. 따라서 이 연구진은 fine-tuning을 할 때 pre-trained 모델은 frozen (얼려두고) 모델 안의 특정 dense layers의 rank decomposition matrices를 최적화 하는 방식을 사용했습니다. Figure 1 이 그 그림인데 왼쪽의 파란색 사각형은 그대로 두고, A, B를 최적화 하는 방식으로 사용했습니다.

Figure 1: Our reparametrization. We only train A and B.

 

 

이러한 방식의 장점으로 총 3가지가 나오게 되는 데

1. pre-trained 모델을 공유해서 작은 LoRA 모듈을 구축하는데 사용될 수 있습니다. 이는 여러 작업에 적응할 수 있습니다. 앞서 언급했던 것처럼 A, B를 교체하면서 작업 전환을 할 수 있습니다.
2. 또한 학습의 효율성을 높여서 하드웨어 요구사항을 3배까지 낮출 수 있습니다.
3. 또한 pre-trained 모델을 동결 시켰고 가중치만 통합을 시켜 inference latency가 발생하지 않습니다.

 

Problem statement

$$ \max_{\Phi} \sum_{(x, y) \in \mathcal{Z}} \sum_{t=1}^{|y|} \log \left( P_{\Phi}(y_t \mid x, y_{<t}) \right) $$

$P_{\Phi} (y|x)$ : pre - trained autoregressive language model

$\mathcal{Z} = \{ (x_i, y_i)\}_{i=1,...,N}$ : 각 하위 작업은 컨텍스트-타겟 쌍의 훈련 데이터셋

$x_i :$ natural language query | $y_i :$ sequences of token

예를 들면 기사를 요약하는 LLM 에서는 $x_i$ 는 기사내용, $y_i$ 는 기사를 요약한 결과 이렇게 해석할 수 있습니다.

이 수식은 기존의 full fine-tuning 방식입니다. 이는 $\Phi_o$ 를 $\Phi_0 + \Delta \Phi$ 로 업데이트를 반복하면서 진행하게 됩니다. 이는 각 하위 테스트 마다 서로 다른 $\Phi$ 를 학습 해야한 다는 의미입니다.

$$ \max_{\Theta} \sum_{(x, y) \in \mathcal{Z}} \sum_{t=1}^{|y|} \log \left( p_{\Phi_0 + \Delta \Phi(\Theta)}(y_t \mid x, y_{<t}) \right) $$

이 논문에서는 $\Delta \Phi = \Delta \Phi (\Theta)$ 를 사용했습니다. parameters $\Theta$ 는 훨씬 작은 사이즈의 파라미터입니다. $\| \Theta \| \ll \| \Phi_0 \|.$ 즉 특정 작업에 맞게 필요한 매개변수 변화를 훨씬 작은 매개변수의 집합인 $\Theta$ 로 표현하는 방법을 제안했습니다.

 

 

 

선행연구

전이 학습(transfer learning) 이 도입 된 이후 모델 적응을 더 효율적으로 하기 위해 많은 연구가 있었습니다.

대표적으로 어댑터 계층 추가(Adapter layers) 추가하는 방법이 있습니다. 모델 구조에 새로운 adapter layers 를 삽입하여 매개변수 조정을 간소화 하는 방법 입니다. 다른 방법으로는 입력 계층 활성화의 일부 형태를 최적화 하는 방법이 있습니다. 입력 계층의 활성화를 직접 최적화 하여 적응 효율성을 높입니다. 두 방법 모두 한계가 있습니다. 어댑터를 추가하면 모델의 복잡성이 증가할 수 있고, 추론 지연이 발생하여 실시간 성능에 부정적인 영향을 줍니다.

 

Table 1 : Inference latency of a single forward pass

 

Table 1 을 보면 같은 Batch size 와 Sequence Length 를 가져도 Adapter 방법이 LoRA 방법에 비해 더 지연시간이 작다는 것을 알 수 있습니다.

다른 방법으로는 입력 계층 활성화의 일부 형태를 최적화 하는 방법이 있습니다. 입력 계층의 활성화를 직접 최적화 하여 적응 효율성을 높입니다.

 

 

Proposed Method

제안한 방법은 pre-trained 된 뉴럴 네트워크 자체는 Dense layers로 구성되 있습니다. 그런데 선행 연구에 의해 알아보면이 pre-trained 모델의 intrinsic dimension 에 중요한 정보들이 모여 있어 차원을 축소하더라도 효율적으로 학슴 할 수 있음을 의미합니다.

따라서 LoRA 의 접근법은 사전 학습된 weight metrices를 $W_0$ 라고 하면 $\mathbf{W}_0 \in \mathbb{R}^{d \times k}$ 의 업데이트를 아래와 같이 저랭크 분해로 제한합니다. 이를 수식으로 나타내면 아래와 같습니다.

$$ \mathbf{W}_0 + \Delta \mathbf{W} = \mathbf{W}_0 + \mathbf{B}\mathbf{A} $$

$$ \mathbf{B} \in \mathbb{R}^{d \times r}, \quad \mathbf{A} \in \mathbb{R}^{r \times k} , \quad r \leq \min(d, k)

$$

따라서 Training을 하는 동안 $W_0$ 는 고정합니다. 즉 그레디언트의 업데이트를 받지 않고, A 와 B 만 학습 가능한 매개변수로 설정합니다. 그럼 input vector $x$ 에 의해서 아래 수식과 같은 결과를 얻ㄹ을 수 있습니다.

$$ h = \mathbf{W}_0 \mathbf{x} + \Delta \mathbf{W} \mathbf{x} = \mathbf{W}_0 \mathbf{x} + \mathbf{B}\mathbf{A}\mathbf{x}  $$

초기화를 할 때는 $A$ 는 랜덤 가우시안 분포로 초기화를 하고, $B$ 는 0으로 초기화를 합니다. 따라서 초기의 $\Delta W = BA = 0$ 이 됩니다. 또한 여기서 $\Delta W x$ 를 $\frac{\alpha}{r}$ 로 스케일링을 합니다. 여기서 $\alpha$ 는 $r$ 에 비례하는 상수 입니다. 이는 다양한 $r$ 값에서도 업데이트 크기를 일정하게 유지할 수 있습니다. 이는 $r$ 가 작거나 클 때 $BA$ 가 생성하는 업데이트 값의 크기가 과도하게 커지거나 작아지는 것을 막아 안정적으로 업데이트를 할 수 있습니다. 이런 적절한 초기화 와 스케일링을 통해 learning rate 조정이 필요하지 않게 만듭니다.

 

 

작업 전환의 효율성

 

작업 전환의 과정은 다음과 같습니다. 만약 다른 down stream task로 변환을 하려면 기존의 $\Delta = BA$ 를 제거 하고 새롭게 업데이트 된 가중치인 $B' A'$ 를 추가하면 됩니다.

$$ W = W_0 + B'A' $$

로 표현할 수 있습니다. 이렇게 $BA$를 빼고 $B'A'$ 를 더하는 연산은, 빠르고 메모리 요구량이 적어 효율성을 높입니다.

 

 

추론 지연

 

LoRA 방법은 $W = W_0 + BA$ 기존 모델을 $W_0$ 를 유지하고 있기 때문에 추론할 때도 기존 모델의 구조를 그대로 유지합니다. 따라서 추가적인 계층이나 연산이 필요하지 않습니다.

 

Transformer 에 LoRA 적용

Transformer 아키텍처에서 적용 가능한 부분 Self-Attention 모듈의 가중치 행렬인 $\{ W_q \ , W_k ,W_v, W_o \}$ {Query, Key, Value, Output} 가 있습니다. LoRA 는 $\{ W_q \ , W_k ,W_v, W_o \}$ 중 하나를 선택하여 단일 행렬로 간주하고 적용합니다. 그리고 MLP 모듈은 고정한 상태로 유지합니다.

 

 

실용적인 이득 및 한계

LoRA 를 사용함으로써 얻을 수 있는 이점으로는 메모리와 저장소 사용량 감소 입니다. 이는 저처럼 LLM을 fine-tuning 하려고 하면 Out of memory Error 가 뜨는 사람이겐 한줄기 의 빛 같은 방법입니다. LoRA를 사용하면, 고정된 매개변수에 대해 optimizer 상태를 저장할 필요가 없어 VRAM 사용량이 크게 줄어듭니다. 예를 들면 GPT-3 175B 모델에서 VRAM 사용량을 1.2TB에서 350GB로 감소시킬 수 있습니다.

$r = 4$ 로 설정하고 Query 및 Value 투영 행렬만을 적응시키는 경우, 체크포인트 크기는 약 10,000배 감소합니다(350GB → 35MB).

한계로는 서로 다른 $A$ 와 $B$ 를 사용하는 다양한 작업(tasks) 을 $W$ 에 병합하면 성능 최적화를 위해 추론 속도를 죽일 수 있지만 이 입력 데이터를 단일 순방향 패스로 배치 처리하긴 어렵다고 합니다. 즉 서로 다른 작업에 필요한 설정이 다르면 이를 처리하긴 어렵다는 의미 입니다.

 

 

 

 

적용 결과

Table 2: 이 표는 RoBERTa-base , RoBERTa-large , 그리고 DeBERTa-XXL 모델이 GLUE 벤치마크 에서 다양한 적응(adaptation) 방법을 사용할 때의 성능을 비교합니다.

 

Figure 2: GPT-3 175B validation accuracy vs. number of trainable parameters of several adaptation methods on WikiSQL and MNLI-matched.

 

 

Figure 2 는 LoRA 가 Training parameters 대비 높은 성능을 보여준다는 의미 입니다. 논문에 접속해서 살펴보면 LoRA를 썼을 때 일관된 결과를 보인다는 것을 논문에서 주장합니다.

 

 

Low-Rank Update

그래서 Low-Rank update 의 특성을 이해하기 위해서 아래의 질문에 대한 연구를 수행 했습니다.

1. 주어진 매개변수 예산(parameter budget) 내에서, 사전 학습된 Transformer의 어떤 가중치 행렬 서브셋(subset)을 적응 시키는 것이 하위 작업 성능을 극대화할 수 있을까? 즉 Transformer 의 $\{ W_q \ , W_k ,W_v, W_o \}$ 중 어떤 가중 치를 적응 시키는 것이 좋을까? 입니다.
2. Optiaml adaption matrix 인 $\Delta W$ 가 정말로 rank-deficient 한가? 그렇다면 실제로 사용할 만한 적절한 rank 는 무엇인가? 여기서 rank-deficient 는 실질적인 차원(effective dimension) 이 실제 차원보다 훨씬 낮은지 보는 것 입니다.
3. $\Delta W$ 와 $W$ 는 얼마나 높은 상관성을 가지는가? 접점이 있는가? 크기는 얼마나 차이나는가?

 

 

어떤 weight Matrices 가 LoRA에 적용 되는가??

Parameter budget 을 18M 으로 고정시키고, r=8 , r=4, r=2 나눠서 weight Matrices 에 적용했을 때의 결과입니다.

 

Table 5: Validation accuracy on WikiSQL and MultiNLI after applying LoRA to different types of attention weights in GPT-3, given the same number of trainable parameters.

 

 

위 결과를 해석해보면 단일 가중치 행렬에 대한 적응 모든 매개변수 중 $W_q , W_k$ 에만 할당할 경우 성능이 크게 저하 되는 거을 알 수 있습니다. 이는 단일 유형의 가중치 행렬만 적응 시키는 것이 정보 표현 측면에서 제한적임을 보입니다.

또한 $r =4$ 를 사용하고 $W_q, W_v$ 둘다 적응시키는 방식이 좋은 결과를 보입니다. 이는 하위 작업에서 다양한 가중치 행렬에 걸쳐 정보를 분산 시키는 것이 효율적임을 보입니다. 그리고 4가지 weight matrices를 다 사용했을 때와 비슷한 결과를 보입니다.

이는 $r=4$ 경우에도 $\Delta W$ 에 충분한 정보가 들어가서 더 높은 rank 를 가진 단일 가중치 행렬보다 적응 성능이 우수한 것을 보입니다 . 따라서 rank 를 낮게 설정하더라도 여러 가중치 행렬을 동시에 적으시키는 것이 효과적임을 보입니다.

 

 

LoRA 를 위한 Optimal Rank : r

이번엔 rank 가 모델 성능이 어떤 영향을 미치는 지 한번 보려고 합니다. \{ W_q , W_v \} , \{W_q, W_k, W_v, W_c \} , W_q 이렇게 3가지 형태로 적응을 시켜보았습니다. ​

Table 6: Validation accuracy on WikiSQL and MultiNLI with different rank r

이 Table 6 의 결과에서 LoRA 를 적용했을 때 $r$ 이 매우 작아도 일때도 놀라운 성능을 보여줍니다. 이는 앞서 말씀드린 $\Delta W$ 의 intrinsic rank 가 매우 작다는 선행 연구와 일관된 결과를 보입니다.

그래서 저자는 , random seed 이 다른 환경에서 와 $r$ 을 다르게 선택했을 때 subspace 가 겹치는 지를 확인해봅니다.

 

 

서로 다른 r 에서 Subspace similarity

서로 다른 $r = 8, r=64$ 로 학습된 adaptation matrices 를 비교 했습니다. singular value decomposition(SVD)를 사용해서 right-singular unitrary matrices $U_{A_{r=8}}, U_{A_{r=64}}$ 를 추출했고, $U_{A_{r=8}}$ 의 상위 $i$ 개의 singular vector 와 $U_{A_{r=64}}$ 의 상위 $j$ 개의 singular vector 와 얼마나 겹치는 지 계산 했습니다.

$$ \phi(A_{r=8}, A_{r=64}, i, j) = \frac{\left\| U_{A_{r=8}}^i{}^\top U_{A_{r=64}}^j \right\|_F^2}{\min(i, j)} \in [0, 1] $$

$\phi (\cdot)$ 은 [0,1] 사이의 값이고 1은 완전히 겹친것이고 0은 완전히 분리된 것입니다.

 

 

 

Figure 3: Subspace similarity between column vectors

 

따라서 결과를 살펴보면 Figure 3 의 왼쪽 두 그래프를 살펴보면 i, j 가 작을 수록 \Theta \approx 1 인 것을 확인할수 있습니다. 이는 r = 8 에서 대부분의 중요한 정보는 이미 얻을 수 있고, r = 64 로 증가시켜도 의미 있는 추가 정보가 포함되지 않는다는 것을 의미합니다. 즉 r 을 불필요하게 높게 설정할 필요가 없습니다.

 

 

 

서로 다른 random seeds 에서 subspace similarity

Figure 4: Left and Middle: Normalized subspace similarity between the column vectors of Ar=64 from two random seeds, for both Wq and Wv in the 48-th layer. Right: the same heat-map between the column vectors of two random Gaussian matrices.

 

 

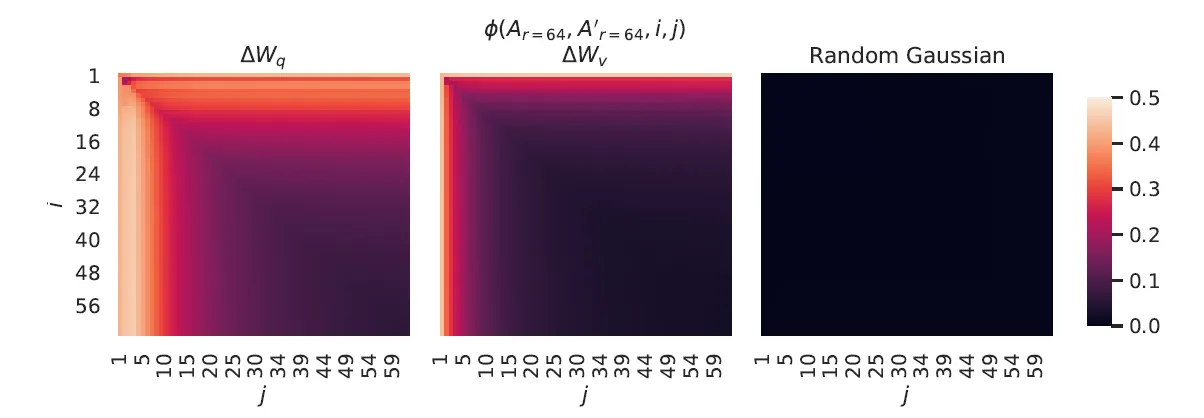
Figure 4 에서 r = 64 로 학습된 두 random seeds 실행 간의 정규화 된 subspaces 의 유사성을 시각화 했습니다. 이때 random gausian matrices 는 완전 무작위 데이터를 생성하고, sigular value direction 을 공유하지 않습니다. Table 6 의 결과에서도 알 수 있듯이 W_q 는 W_v 보다 더 높은 ‘intrinsic rank’ 를 가지고 있습니다. 이는 \Delta W_q 가 더 많은 공통 특이값 방향(singular value directions)을 학습했음을 보입니다. 즉 더 많은 정보를 학습한 다는 의미 입니다.

 

 

 

마지막으로 얼마나 연관되어있는지를 확인하기 위해서 $||U^\top W_q V^\top||F$ 와 $||W||{F}$ 를 비교했습니다. $||U^\top W_q V^\top||_F$ 이 값이 클수록 $\Delta W_q$ 와 $W_q$ 사이의 연관성이 더 크다는 것을 의미합니다.

 

Table 7: The Frobenius norm of $U^\top W_q V^\top$where $U$ and $V$ are the left/right top r singular vector directions of either (1) $W_q$, (2) $W_q$, or (3) a random matrix.